https://github.com/l-paz91/principles-practice/tree/master/Graphics%20Files
Chapter 13 // Exercise 19
Define a class Star. One parameter should be the number of points. Draw a few stars with differing numbers of points, differing line colours, and differing fill colours.
Github: https://github.com/l-paz91/principles-practice/tree/master/Chapter%2013/Exercise%2018
For this one, I decided that the minimum number of points needed was 5. After that, I found a chapter from a book called "Connections: The Geometric Bridge Between Art and Science" by Jay Kappraff. They explain that any polygon with 5 or more vertices can be used to create star polygons by extending the lines of each side till they intersect.
I also found this excellent video https://www.youtube.com/watch?v=omsNTaNLvAA which shows how to create stars from regular polygons by skipping vertices n number of times for each polygon. This video also helped visualize the difference between a real star polygon and a degenerate star polygon.
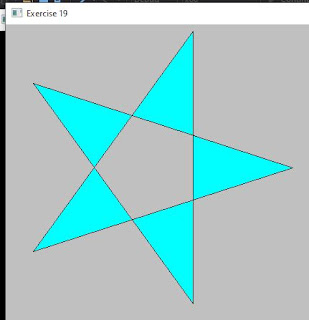
In the end though I decided to use a function I created in an earlier exercise that finds any point on a circle given an angle. Given the number of points, each point is n angle away from each other. So I can tell this function to keep retrieving me new points until we have enough to make the star.
This works perfectly with real star polygons, however the draw_lines() function needs to be modified to fill the star in. It doesn't work for degenerate star polygons though. After some thinking I decided to go a bit simpler and create an outer circle and an inner circle. Then advance the rotation by n degrees each time selecting points alternatively on the outer and inner circle and then connecting them up. Not only does this allow 4 pointed stars but it works with both real star polygons and degenerate star polygons and draw_lines() doesn't have to modified:
(EDIT - please ignore the inner circle in this photo, it has nothing to do with the inner circle of the star...I just forgot to remove it)
I also changed the constructor so you can change the outer/inner radii and added a starting angle so you can rotate the star:
I also found this excellent video https://www.youtube.com/watch?v=omsNTaNLvAA which shows how to create stars from regular polygons by skipping vertices n number of times for each polygon. This video also helped visualize the difference between a real star polygon and a degenerate star polygon.
In the end though I decided to use a function I created in an earlier exercise that finds any point on a circle given an angle. Given the number of points, each point is n angle away from each other. So I can tell this function to keep retrieving me new points until we have enough to make the star.
This works perfectly with real star polygons, however the draw_lines() function needs to be modified to fill the star in. It doesn't work for degenerate star polygons though. After some thinking I decided to go a bit simpler and create an outer circle and an inner circle. Then advance the rotation by n degrees each time selecting points alternatively on the outer and inner circle and then connecting them up. Not only does this allow 4 pointed stars but it works with both real star polygons and degenerate star polygons and draw_lines() doesn't have to modified:
(EDIT - please ignore the inner circle in this photo, it has nothing to do with the inner circle of the star...I just forgot to remove it)
I also changed the constructor so you can change the outer/inner radii and added a starting angle so you can rotate the star:




No comments:
Post a Comment