https://github.com/l-paz91/principles-practice/tree/master/Graphics%20Files
Chapter 13 // Exercise 3
Define a class Arrow, which draws a line with an arrowhead.
Github: https://github.com/l-paz91/principles-practice/tree/master/Chapter%2013/Exercise%203
Again, I wanted to give a way to adjust the size of the arrow head so this took a little longer as I thought about it. Then as I spent a few hours banging my head against the wall I began to realise that this would take quite a bit of maths to solve. But I didn't know what maths. After more hours of googling I came across this stack overflow post which started to make some sense:
https://stackoverflow.com/questions/10316180/how-to-calculate-the-coordinates-of-a-arrowhead-based-on-the-arrow
I knew there had to be some vector stuff involved as when I went down the trigonometry route; I discovered that the two "back points" could potentially be infinite between the mid-base point of the triangle and the tip.
With vectors though (not std::vector), the direction of the arrow helps narrow down those two back points. Eventually I came across this post:
https://math.stackexchange.com/questions/927802/how-to-find-coordinates-of-3rd-vertex-of-a-right-angled-triangle-when-everything?rq=1
Which started to give me some actual formulas and "normal-ish" words to try and figure out what I had to do. And then I found this post off the side of it:
https://math.stackexchange.com/questions/2125690/find-coordinates-of-3rd-right-triangle-point-having-2-sets-of-coordinates-and-a
This link was the jackpot. Thank you Stack Exchange user Futurologist, you're a genius. This formula was exactly what I had been looking for.
Here is one of the arrows drawn by my program (with some annotations in paint):
We know the locations of the following points:
x1, y1 == p1.x, p1.y
x2, y2 == p2.x, p2.y
x3, y3 == p3.x, p3.y
I wanted the arrow tip to be at P2 with each side of the arrow to have a length of arrowSize. Point 3 was found by using a formula to find a point on a line given two points, the full distance and the distance away from Point 2.
The exact formula above produced the correct Y results but the X ones were a little off. I figured it was because the triangle was slightly different. I ended up using Point 3 (instead of x2,y2) to get the co-ordinates I was looking for. This gave me the left hand corner and to get the right; I simply reversed the P1 and P2 coordinates.
I started this at 4pm and just finished writing this post at 12:30am. At least I've learnt something extremely useful.
The arrow can change size, have a different fill colour to line colour, have the line style changed to dashes/dots, and increase/decrease the weight of the line; whatever takes your fancy.
https://stackoverflow.com/questions/10316180/how-to-calculate-the-coordinates-of-a-arrowhead-based-on-the-arrow
I knew there had to be some vector stuff involved as when I went down the trigonometry route; I discovered that the two "back points" could potentially be infinite between the mid-base point of the triangle and the tip.
With vectors though (not std::vector), the direction of the arrow helps narrow down those two back points. Eventually I came across this post:
https://math.stackexchange.com/questions/927802/how-to-find-coordinates-of-3rd-vertex-of-a-right-angled-triangle-when-everything?rq=1
Which started to give me some actual formulas and "normal-ish" words to try and figure out what I had to do. And then I found this post off the side of it:
https://math.stackexchange.com/questions/2125690/find-coordinates-of-3rd-right-triangle-point-having-2-sets-of-coordinates-and-a
This link was the jackpot. Thank you Stack Exchange user Futurologist, you're a genius. This formula was exactly what I had been looking for.
Here is one of the arrows drawn by my program (with some annotations in paint):
We know the locations of the following points:
x1, y1 == p1.x, p1.y
x2, y2 == p2.x, p2.y
x3, y3 == p3.x, p3.y
I wanted the arrow tip to be at P2 with each side of the arrow to have a length of arrowSize. Point 3 was found by using a formula to find a point on a line given two points, the full distance and the distance away from Point 2.
The exact formula above produced the correct Y results but the X ones were a little off. I figured it was because the triangle was slightly different. I ended up using Point 3 (instead of x2,y2) to get the co-ordinates I was looking for. This gave me the left hand corner and to get the right; I simply reversed the P1 and P2 coordinates.
I started this at 4pm and just finished writing this post at 12:30am. At least I've learnt something extremely useful.
The arrow can change size, have a different fill colour to line colour, have the line style changed to dashes/dots, and increase/decrease the weight of the line; whatever takes your fancy.

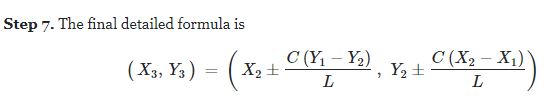

No comments:
Post a Comment