https://github.com/l-paz91/principles-practice/tree/master/Graphics%20Files
Chapter 14 // Exercise 7
Define a Striped_closed_polyline using the technique from Striped_rectangle (this requires some algorithmic inventiveness).
Github: https://github.com/l-paz91/principles-practice/tree/master/Chapter%2014/Exercise%207
I'm not quite sure how I solved this one. It feels like I stumbled across the right answer somehow. It took some serious debugging to figure out what I was doing wrong (especially when I was almost there but a few lines kept being off by 1 pixel...)
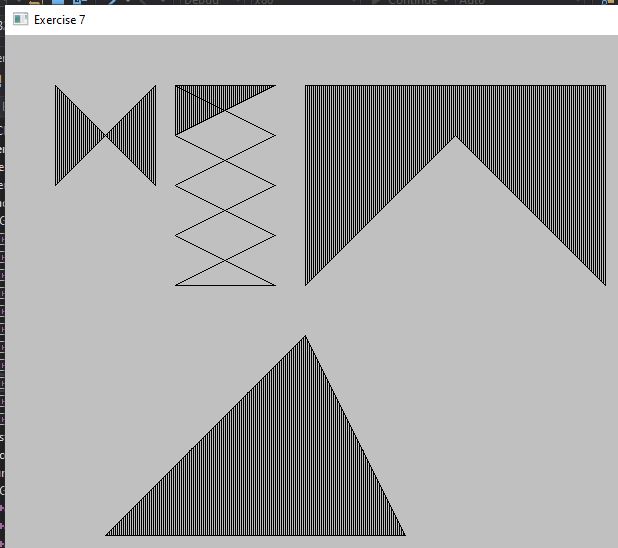
I started off by creating a bounding box for the polygon. That way I could draw a line and see if it intersects with another line (this returns where the intersection happened). This is due to the fact that a closed_polyline might have gaps in it.
I then used the code from striped_rectangle to see how it looks:
This gave the line pattern; I just needed to figure out a way of only drawing part of it. I decided to go loop through each stripe and see if it hit the lines in the shape and push the intersection point back into a vector. Because it was testing each stripe individually the intersect points are pushback in order of corresponding x and y points. In some cases however, this can give more than 2 intersections.
I am however stuck on shapes that have multiple intersections. To be honest I would just do a design like this in Photoshop or create a vector image in Illustrator. I feel this is adequate enough for the exercise.
I suppose eventually though I could write a new intersect function that checks for multiple line intersection and returns the closest intersection.
I started off by creating a bounding box for the polygon. That way I could draw a line and see if it intersects with another line (this returns where the intersection happened). This is due to the fact that a closed_polyline might have gaps in it.
I then used the code from striped_rectangle to see how it looks:
This gave the line pattern; I just needed to figure out a way of only drawing part of it. I decided to go loop through each stripe and see if it hit the lines in the shape and push the intersection point back into a vector. Because it was testing each stripe individually the intersect points are pushback in order of corresponding x and y points. In some cases however, this can give more than 2 intersections.
I am however stuck on shapes that have multiple intersections. To be honest I would just do a design like this in Photoshop or create a vector image in Illustrator. I feel this is adequate enough for the exercise.
I suppose eventually though I could write a new intersect function that checks for multiple line intersection and returns the closest intersection.




No comments:
Post a Comment