https://github.com/l-paz91/principles-practice/tree/master/Graphics%20Files
Chapter 12 // Exercise 11
Draw a series of regular polygons, one inside the other. The innermost should be an equliateral triangle, enclosed by a square, enclosed by a pentagon, etc. For the mathematically adept only: let all the points of each N-polygon touch sides of the (N+1)-polygon.Hint: The trigonometric functions are found in <cmath> (Section 24.8, Appendix B.9.2)
Github: https://github.com/l-paz91/principles-practice/blob/master/Chapter%2012/Exercise%2011/Exercise%2011%20-%20Complete
This exercise reminded me of when I first read some of the exercises in Chapter 4 way back in 2016; I was scared and convinced I couldn't do it. I'm also mathematically inept so the second portion of the exercise really threw me off. This was one of those exercises that really threw me out of my comfort zone and I had to go off and do some research to figure out what he was talking about.
I once again turned to Maths Is Fun to figure out what the hell I had to do.
https://www.mathsisfun.com/geometry/regular-polygons.html
After about an hour of reading and re-reading I managed to grasp that a regular polygon means everything is equal (I know, it's big brain time). The sides will always be the same length as all the others. With this in mind I started off by writing a little program that given the end points of a line, an angle and a length; it will draw the next line:
I was very happy when this worked. I'm terrible at this kind of stuff. You can find the code for this here:
https://github.com/l-paz91/principles-practice/blob/master/Chapter%2012/Exercise%2011/11.1
This is tedious though and error prone. Maths is Fun state how each point on a regular polygon can be found on the circumference of a circle. Therefore, given a centre point, radius and the number of sides, we can effectively work out each point in the polygon. These points can then be added to the Polygon type to draw one for us instead of using lines.
The code for this example can be found here:
https://github.com/l-paz91/principles-practice/blob/master/Chapter%2012/Exercise%2011/11.2
The important part is dividing the current side number by the overall number of sides each time to determine the next point. I am terrible at maths; I'm still not 100% sure how this is working. I eventually ended up adapting code from here to get this to work:
https://stackoverflow.com/questions/7198144/how-to-draw-a-n-sided-regular-polygon-in-cartesian-coordinates
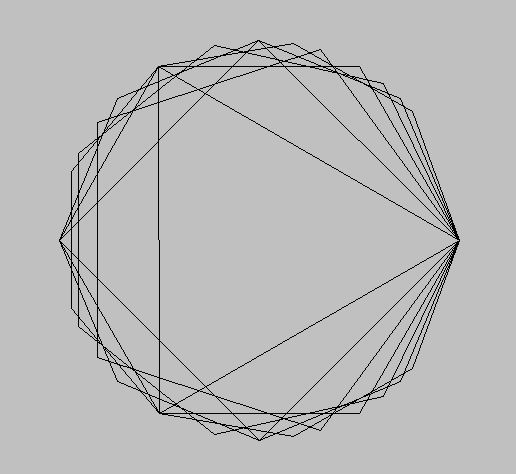
The last part was then putting this in a loop and drawing as many polygons as we can! What's interesting to note though is that at a certain point, you will have a pretty solid circle and will become difficult to pick out all the individual polygons:
10 Polygons:
20 Polygons:
After all that, this exercise took me a good 5 hours in total but I'm glad I finished it as this stuff is actually extremely useful for game development.
Another tip. You can change the rotation of the polygons by adding an angle to the new x an y co-ordinates in makePolygon(). Remember, the C++ standard library uses radians not degrees.
EDIT 29/03/2020: After letting my brain decompress, I realised that I still haven't actually done what he asked for in either scenarios. I hadn't placed polygons inside one another nor does each point touch the sides of the n+1 polygon.
So, to draw polygons inside each other I modified the code slightly to increase the radius each time:
And to make it so all the points touch the sides of the outer polygon, then the radius of the inside polygon must match the radius of the apothem of the outer polygon...damn this makes me sound smart.
We know for sure the radius of the polygon so we can use this formula to find the apothem:
All the points can't actually touch the sides of the outer polygon otherwise they would no longer be regular polygons but now each polygon is perfectly sized to fit within the incircle circumference of the outer polygon:
I once again turned to Maths Is Fun to figure out what the hell I had to do.
https://www.mathsisfun.com/geometry/regular-polygons.html
After about an hour of reading and re-reading I managed to grasp that a regular polygon means everything is equal (I know, it's big brain time). The sides will always be the same length as all the others. With this in mind I started off by writing a little program that given the end points of a line, an angle and a length; it will draw the next line:
I was very happy when this worked. I'm terrible at this kind of stuff. You can find the code for this here:
https://github.com/l-paz91/principles-practice/blob/master/Chapter%2012/Exercise%2011/11.1
This is tedious though and error prone. Maths is Fun state how each point on a regular polygon can be found on the circumference of a circle. Therefore, given a centre point, radius and the number of sides, we can effectively work out each point in the polygon. These points can then be added to the Polygon type to draw one for us instead of using lines.
The code for this example can be found here:
https://github.com/l-paz91/principles-practice/blob/master/Chapter%2012/Exercise%2011/11.2
The important part is dividing the current side number by the overall number of sides each time to determine the next point. I am terrible at maths; I'm still not 100% sure how this is working. I eventually ended up adapting code from here to get this to work:
https://stackoverflow.com/questions/7198144/how-to-draw-a-n-sided-regular-polygon-in-cartesian-coordinates
The last part was then putting this in a loop and drawing as many polygons as we can! What's interesting to note though is that at a certain point, you will have a pretty solid circle and will become difficult to pick out all the individual polygons:
10 Polygons:
20 Polygons:
After all that, this exercise took me a good 5 hours in total but I'm glad I finished it as this stuff is actually extremely useful for game development.
Another tip. You can change the rotation of the polygons by adding an angle to the new x an y co-ordinates in makePolygon(). Remember, the C++ standard library uses radians not degrees.
EDIT 29/03/2020: After letting my brain decompress, I realised that I still haven't actually done what he asked for in either scenarios. I hadn't placed polygons inside one another nor does each point touch the sides of the n+1 polygon.
So, to draw polygons inside each other I modified the code slightly to increase the radius each time:
And to make it so all the points touch the sides of the outer polygon, then the radius of the inside polygon must match the radius of the apothem of the outer polygon...damn this makes me sound smart.
We know for sure the radius of the polygon so we can use this formula to find the apothem:









No comments:
Post a Comment