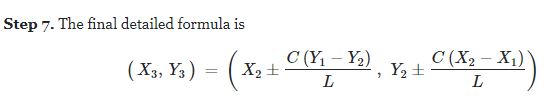https://github.com/l-paz91/principles-practice/tree/master/Graphics%20Files
Chapter 13 // Exercise 6
Write a program that draws a class diagram like the one in Section 12.6. It will simplify matters if you start by defining a Box class that is a rectangle with a text label.
Github: https://github.com/l-paz91/principles-practice/tree/master/Chapter%2013/Exercise%206
I originally decided to derive the Box class and add text to it, however it proved a little cumbersome. So instead, I derived the Text class and gave it a Box as a member variable. The only difficult part was giving the box the correct length. I tried searching the FLTK documentation however there is no way to get the full length the Text string. There is a function called fl_width() which takes in a char and calculates the width of it in pixels using the font size given however, it always returned -1 for me so I don't think it works properly. So instead, I made the width the number of characters multiplied by the font size. It isn't perfect but it ensures the text box is always big enough.
EDIT 12/05/2020
So I found out the reason fl_width() is returning -1 is because the font_descriptor() is null in the graphics driver. This is because the font is never actually set, we just call the default Font constructor in Text::draw_lines().
To enable fl_width() to work the font must be intialised in the text constructor.
fl_width() then takes in a c-style string and determines the width of pixels in each character. This does not account for spacing though so in some cases the box may not encapsulate the text. for this I just added on some padding. Not perfect but close enough.
I provided a function in the Text class to be able to do this:
EDIT 12/05/2020
So I found out the reason fl_width() is returning -1 is because the font_descriptor() is null in the graphics driver. This is because the font is never actually set, we just call the default Font constructor in Text::draw_lines().
To enable fl_width() to work the font must be intialised in the text constructor.
fl_width() then takes in a c-style string and determines the width of pixels in each character. This does not account for spacing though so in some cases the box may not encapsulate the text. for this I just added on some padding. Not perfect but close enough.
I provided a function in the Text class to be able to do this: